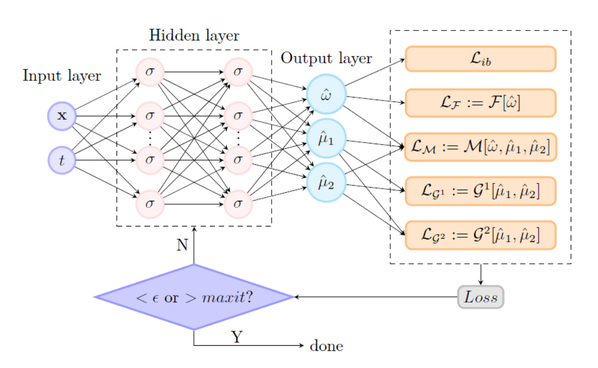
Recently, the research team of partial differential equation, comprising Dr. Wang Ming, Prof. He Guoliang, and Dr. Xu Tao from the School of Mathematics and Information Science at ZZULI, published a research paper titled "Localized waves for modified Boussinesq equation and Mikhailov-Lenells equation based on Physics-informed neural networks and Miura transformation" in Chaos, Solitons & Fractals (Chinese Academy of Sciences Q1, IF = 19.0), a top-tier international journal. Dr. Wang Ming serves as the first author, Prof. He Guoliang as the corresponding author, and ZZULI as the first affiliated institution.

In the field of integrable system, the research on nonlinear localized waves is conducive to the understanding of the dynamic mechanisms of nonlinear systems, rendering theoretical support for studies in fiber optic communication, tsunami, and other areas. How to attain new localized waves for nonlinear models remains a prominent research focus. To address this issue, the team leveraged the Miura transformation, a classic theory concerning integrable systems, and embedded it into physics-informed neural networks. This approach enabled the construction of a neural network algorithm effective in simultaneously training two models. Starting from the initial boundary value condition of the classical Boussinesq equation, the team delved into a new localized wave excitation mechanism for two coupled systems, i.e., the modified Boussinesq equation and the Mikhailov-Lenells equation. Through nonlinear one-to-many mappings, the team acquired multiple new localized wave structures under unsupervised training, including anti-dark solitons and anti-kink solitons. This article represents another research outcome of the team following its paper titled "Data-driven localized waves of a nonlinear partial differential equation via transformation and physics-informed neural network" published in Nonlinear Dynamics (Chinese Academy of Sciences Q2, IF = 5.2) 113 (2025) 2559-2568 in 2025.

This research has been supported by such projects as the National Natural Science Foundation of China and the Natural Science Foundation of Henan Province.

Journal article link: https://www.sciencedirect.com/science/article/pii/S096007792401316X